
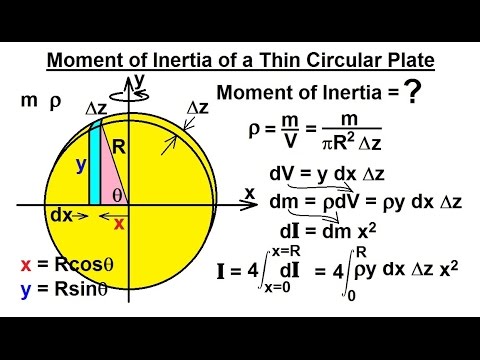
It is given as:ĪBCD is a sector with area = (r⋅d θ) ⋅ dr = r ⋅ drd θ We need to determine the differential area by finding the area of the element.
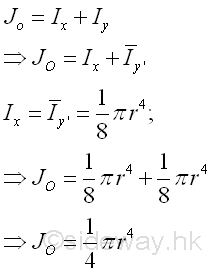
M.O.I relative to the origin, Jo = I x + I y = ⅛ πr 4 + ⅛ πr 4 = ¼ πr 4 Derivation of Formula for Moment of Inertia of Semicircleįor deriving the moment of inertia of semicircle we define the coordinates using the polar system. In order to find the moment of inertia of the semicircle, we will take the sum of both the x and y-axis. As a result, M.O.I will be half the moment of inertia of a full circle. Because the semi-circle rotating around an axis is symmetric in this case, we consider these values to be equal. Likewise, for the semicircle, the x-axis moment of inertia equals the y-axis moment of inertia. Then, we need to pull out the area of a circle which gives us: Now, the M.O.I relative to the origin, Jo = I x + I y = ¼ πr 4 + ¼ πr 4 = ½ πr 4 To establish the moment of inertia of the semi-circle, we will add the x and y axes.īecause of complete symmetry and uniform area distribution, we know that the moment of inertia relative to the x-axis is equal to that of the y-axis for a full circle. To obtain the value of the moment of inertia of semicircle, initially derive the results of the moment of inertia of a full circle and divide it by two for getting the desired result of that moment of inertia for a semicircle. Let’s take consideration of a physical body that has a mass of m.I = πr 4 / 4 Finding Moment of Inertia of Semicircle We denote the Mass Moment of Inertia by I The Mass Moment of Inertia of the physical object is expressible as the sum of Products of the mass and square of its perpendicular distance through the point that is fixed (A point which causes the moment about the axis passing through it). The physical object is made of the small particles.

This is because it is the resistance to the rotation that the gravity causes. We can measure the moment of inertia by using a simple pendulum.


 0 kommentar(er)
0 kommentar(er)
